气柜外压作用下的有限元分析
2015/8/14 9:24:57 点击: 文章来源:www.jshhcc.com
由于本研究的气柜钟罩失效形式属于外压作用下的失稳,即失效时产生了较大的变形,因此此类问题可归结为非线性问题,需采用非线性分析方法来进行。应该注意:进行非线性有限元分析所采用的应力一应变曲线应该采用材料的真实应力一应变曲线。
1、建立有限元计算模型
由于气柜实际结构的轴对称性,有限元计算模型采用图3所示的轴对称模型。
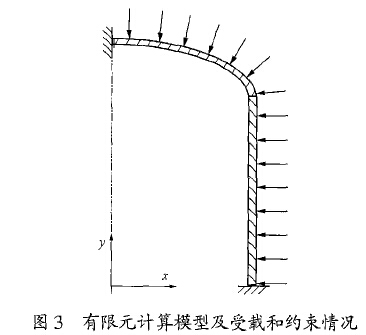
由于板壳单元无法实现容器器壁的径向分层,因此对压力容器进行有限元分析时,一般采用三维实体单元,本研究采用4节点单元阮hd42,建立轴对称模型。计算过程中打开自动时间步长和大变形选项。
对本气柜,共划分13936个单元,节点数为17484,在外部施加均布载荷0.O04MP芝,载荷子步为200。
2载荷及边界(约束)条件
对于承受外压的压力容器,其边界条件如图3所示,在对称面上限制法线方向的位移自由度。在ANSYS前处理器中建立其有限元模型,进行网格划分,单元网格划分结果如图4所示。
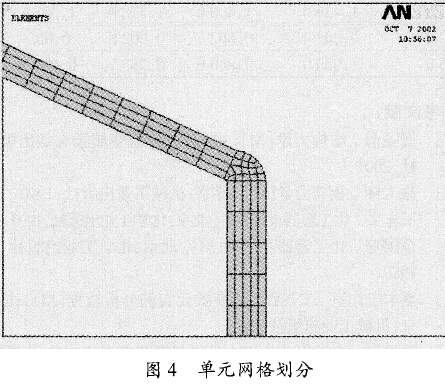

3结果及分析
从有限元分析的结果可以看出,钟罩顶与罩壁结合部位附近的应力、变形均较大(如图5、图6所示),这是由于钟罩顶与钟罩壁的结合处存在结构不连续而导致的,因此该部位属于易发生失效的危险区域。
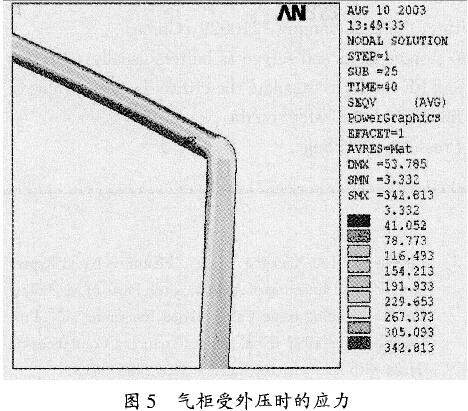
由于此问题属于非线性问题,因此本文利用ANS、侣的时间历程后处理器R万理6,进一步得到计算模型中指定点的分析结果(如变形)与时间的函数关系:首先根据应力以及变形分析的初步结果,找出钟罩在承受外压时的特征部位,该部位的计算结果应该能反映结构的总体变形特征;然后利用时间历程后处理器,以载荷(或时间)作为纵坐标,以特征部位在载荷作用下的位移为横坐标,得到该部位的载荷一位移曲线图。从本研究所涉及的承受外压的钟罩来分析,由于钟罩顶与钟罩壁的结合处存在结构不连续,变形比较明显,如图6所示,因此在钟罩顶边缘附近选取位移最大的节点(节点号:9903),在后处理B泥仓6中作出其载荷一位移曲线,如图7所示。图7载荷一位移曲线由图7可以看出,随着载荷的增加,特征部位的位移逐渐增加,当载荷增加到一定程度时,位移增加比较明显,即结构总体的变形加剧,产生失稳屈曲失效:当外压为0.001MPa时,位移较小,约为6.9~;当外压加至0.002NIPa时,位移增加至15.4~;而当外压为理论临界压力0.002gMI〕a时,变形比较明显,位移为25.5~;此时若继续施加压力,则气柜变形加剧,如当外压为O.004MI〕a时,位移增至53.78~,此时钟罩顶的凹陷已经比较明显。利用回归分析软件对以上结果进行处理,可以得到施加外压和位移的关系曲线,对该关系式进行求导,从导数值的变化情况即可以看出外压与位移变化趋势的关系。本研究对有限元计算结果(图7所示曲线)进行进一步分析,得到该回归曲线的斜率变化情况(见表1),表1给出了外压值从0.00007NIPa到0.003MI〕a之间载荷位移曲线的斜率,可以看出:随着外压增加,斜率减小,即同样的外压增量下,变形量增大,并且在0.0024Nlpa附近,该增大趋势更为明显,即回归曲线斜率变化比较明显时对应的外压值约在0.0024MPa附近。这表明,在该区域,即使外压增加的幅度不大,仍有可能使气柜钟罩产生较大的变形,这一分析结果与理论计算结果亦比较吻合。
结论

结论
a.外压作用下的气柜钟罩顶屈曲失稳,是导致其塌陷的直接原因。
b.本研究对外压作用下,气柜钟罩顶的失稳临界压力进行理论分析计算,得到其理论的临界失稳压力为0.0029MI〕a。
c.本研究利用目前比较流行的应力分析软件AN-SYS6 . 0,对外压作用下的钟罩进行了非线性有限元分析,得到钟罩在外压下的变形情况,以及特征部位单元的载荷一位移曲线,该曲线表征了气柜钟罩在外压作用下的变形情况。
